
ТЕХНИЧЕСКАЯ ИНФОРМАЦИЯ
| ФРЕЗЫ |
| СВЕРЛА |
| РЕЗЦЫ |
| МЕТЧИКИ |
| ПЛАШКИ |
| РАЗВЕРТКИ |
| ПРОТЯЖКИ |
| ЗЕНКЕРЫ |
| Резание металлов |
| ИЗМЕРЕНИЕ |
Общие положения | Оглавление | Условия формообразования поверхностей деталей
Конструкция режущего инструмента
СПОСОБЫ ОБРАЗОВАНИЯ ИСХОДНЫХ ИНСТРУМЕНТАЛЬНЫХ ПОВЕРХНОСТЕЙ
Режущий инструмент можно рассматривать как тело, ограниченное исходной инструментальной поверхностью И, на которой располагаются профилирующие участки режущих кромок, непосредственно формирующие поверхность детали. Так, фреза — это тело вращения, которое ограничено поверхностью вращения И и в процессе обработки касается поверхности детали. Прорезая стружечные канавки и образовывая заднюю поверхность, это тело трансформируется в режущий инструмент.
Метчик можно представлять как винт, сопряженный с обрабатываемой гайкой.
Он превращается в инструмент, образовывая стружечные канавки и создавая задние поверхности зубьев.
Исходная поверхность И в процессе обработки должна касаться поверхности детали.
В процессе обработки поверхность детали Д совершает определенное движение относительно инструмента и занимает ряд последовательных положений. Огибающую поверхность к рассматриваемым последовательным положениям поверхности Д и можно принять за исходную инструментальную поверхность И.
При определении поверхности И как огибающей поверхности Д обычно наблюдается их взаимное касание вдоль линии Е, называемой характеристикой.
Рассмотрим пример определения исходной поверхности И по первому способу для круглой цилиндрической поверхности Д. Будем считать, что схема обработки включает вращение заготовки вокруг ее оси О1 и медленное поступательное движение вдоль этой же оси О1. Пусть инструмент вращается вокруг оси О2, перпендикулярной оси О1. Исходная инструментальная поверхность И как огибающая поверхности детали при ее движении относительно инструмента будет поверхностью тора (рис. 1, а). Она образуется вращением характеристики Е, являющейся окружностью, вокруг оси О3. Если воспроизвести исходную поверхность И в форме рабочей поверхности шлифовального круга, то при рассматриваемой схеме можно будет обработать круглую цилиндрическую поверхность детали Д.
При втором способе образования исходных инструментальных поверхностей (рис. 1, б, в, г) известной считается схема обработки, т. е. движения, совершаемые в процессе обработки заготовкой и инструментом в системе хуz. Сообщим системе хуz некоторое движение и определим вспомогательную производящую поверхность Т как огибающую последовательных положений поверхности детали Д при ее движении относительно движущейся системы хуz. Рассматривая движение вспомогательной производящей поверхности Т относительно инструмента, определяют огибающую поверхность, которую можно принять за исходную инструментальную поверхность, так как она в процессе обработки будет касаться поверхности детали Д.
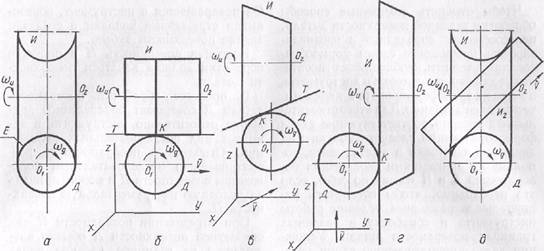
Рис. 1. Способы образования исходных инструментальных поверхностей
Действительно, поверхность Д в каждый момент времени будет иметь со вспомогательной поверхностью Т характеристику Е1, по которой они касаются друг с другом. Исходная поверхность И также будет касаться поверхности Т по характеристике Е2. Так как линии Е1 и Е2 находятся на одной поверхности Т, то они, в общем случае, будут пересекаться в некоторой точке К. В этой точке поверхностей И и Д будет наблюдаться касание.
В рассматриваемом примере обработки круглой цилиндрической поверхности Д системе хуz сообщим поступательное движение параллельно оси O3. Тогда вспомогательной производящей поверхностью будет плоскость Т, параллельная оси O2 и касающаяся поверхности детали Д вдоль ее образующей.
При движении плоскости Т относительно инструмента исходная поверхность как огибающая плоскости Т создается в форме круглой цилиндрической поверхности И. Она касается поверхности детали Д в точке К. Легко понять, что инструмент в форме шлифовального круга, ограниченного исходной поверхностью И, при рассматриваемой схеме будет обрабатывать заданную цилиндрическую поверхность детали Д.
При третьем способе образования исходных инструментальных поверхностей (рис. 1, д) определяется исходная поверхность И1 как огибающая последовательных положений поверхности детали при движении заготовки относительно инструмента. Поверхности И1 сообщается некоторое движение и определяется огибающая, которая может быть принята за исходную инструментальную поверхность И2. В процессе обработки поверхность И2 будет касаться поверхности детали. Действительно поверхность И1 в процессе обработки касается поверхности Д вдоль характеристики Е, а поверхность И2 - поверхности И1 по характеристике Е2. Так как линии Е1 и Е2 находятся на одной поверхности И1 то они пересекаются в некоторой точке К. В этой точке исходная поверхность И2 касается поверхности детали Д.
Рассматривая пример обработки цилиндра Д и образуя исходную поверхность И2 по третьему способу, сообщим поверхности тора И1 поступательное движение под углом к оси О2.
Огибающей поверхностью И1 будет сложная цилиндрическая поверхность И2, которая в любой момент времени будет соприкасаться с поверхностью детали Д в одной точке К. В отличие от предыдущего случая точка контакта К в процессе обработки будет менять свое положение как на исходной поверхности И, так и на поверхности детали Д.
Таким образом, при выбранной схеме обработки могут быть образованы всевозможные исходные поверхности и на их базе спроектированы разнообразные инструменты, предназначенные для обработки заданной поверхности детали Д.
Задачу определения размеров исходных инструментальных поверхностей, которая сводится к отысканию огибающих поверхностей, можно решать различными методами.
Если задано семейство поверхностей уравнением f(xyzt) = 0, то огибающая поверхность будет выражаться системой двух уравнений:
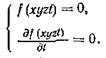
где h - параметр винтового движения.
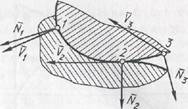
Рис. 2. Кинематическое условие контакта сопряженных поверхностей
Задачу нахождения огибающей поверхности можно решить, используя так называемый кинематический метод.
При движении произвольной поверхности (рис. 2) в рассматриваемых узловых точках вектор скорости U может занимать различное положение относительно нормали N к поверхности. В произвольных точках 1 и 3 поверхности нормаль N не перпендикулярна к скорости V. В окрестности точки 1 при изображенном взаимном расположении векторов N и V будет наблюдаться внедрение соответствующего участка поверхности в близлежащее пространство, а в окрестности точки 3 будет происходить втягивание соответствующего участка внутрь движущейся поверхности. Поэтому точки 1 и 3 не будут точками контакта. На движущейся поверхности можно найти особые точки 2, в которых нормаль N к поверхности будет перпендикулярна скорости V. В точках 2 вектор V попадает в касательную плоскость и поэтому точки 2 будут точками контакта сопряженных поверхностей.
Таким образом, если поверхность Д движется в пространстве и образует огибающую поверхность И, то характеристику в общем случае можно определить как линию, в каждой точке которой вектор относительной скорости V направлен по касательной к поверхности.
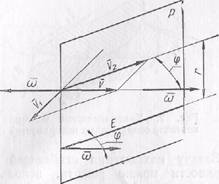
Рис. 3. Определение характеристики при винтовом движении плоскости
Аналитически это условие контакта записывается так:
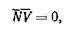
т. е. скалярное произведение вектора нормали N к поверхности детали Д и вектора V скорости относительного движения в точках характеристики Е должно быть равно нулю.
Условие контакта позволяет находить точки контакта сопряженных поверхностей в различные моменты времени. Совокупность точек контакта в системе, связанной с деталью, является поверхностью детали. Совокупность точек контакта в системе, связанной с инструментом, будет исходной инструментальной поверхностью.
При определении огибающих поверхностей И, образующихся при движении поверхности Д, движение поверхности Д можно раскладывать на составляющие. Целесообразно разложение производить таким образом, чтобы одно из составляющих движений вызывало скольжение поверхности Д «самой по себе». Тогда при определении характеристики это движение можно не учитывать. Таким путем сложное движение можно свести к более простому и упростить нахождение характеристики, а следовательно, и огибающей поверхности.
Например, определим характеристику при винтовом движении плоскости Р (рис. 3). Угол между осью винтового движения и плоскостью обозначим ФИ. Винтовое движение плоскости Р будем рассматривать как совокупность прямолинейно-поступательного движения со скоростью V и вращательного с угловой скоростью ОМЕГА.
Движение со скоростью V разложим на два движения:
V=V1+V2
Вектор V1 направим перпендикулярно вектору V, а вектор V2 расположим в плоскости Р. Движение со скоростью V2 приводит к перемещению плоскости Р «самой по себе», поэтому его при определении характеристики можно неучитывать. Длина вектора V1 будет равна:
V1=V*tg(ФИ)
Движение со скоростью V1 можно представить как пару вращения, у которой векторы угловой скорости примем равными ФИ. Тогда расстояние между ними будет равно:
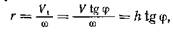
где h - параметр винтового движения.
Заданный вектор ОМЕГА угловой скорости вращения плоскости Р и один из векторов пары вращения взаимно уравновешиваются. Таким образом, винтовое движение плоскости сведено к одному вращательному движению. Характеристикой Е в этом случае будет ортогональная проекция оси вращения на плоскость Р, т. е. линия, отстоящая от проекции оси винтового движения на расстоянии r и составляющая с ней угол ФИ.
В результате винтового движения характеристики вместе с плоскостью Р создается огибающая поверхность, которая является винтовой эвольвентной поверхностью, радиус основного цилиндра которой равен r.
Общие положения | Оглавление | Условия формообразования поверхностей деталей
|
ПРОДАЖА инструмента |
Copyright © 2007-2009, Фреза, сверло, метчик, плашка, развертка, резцы и другой инструмент в Москве. All rights reserved